Advanced Prescriptive Data Analytics
I am currently engrossed in the realm of prescriptive data analytics, focusing on the development of innovative frameworks and algorithms that are pivotal in extracting value, generating revenue, and providing profound insights from complex data sets.
Extensive Computational Experiments for Robust Statistical Evaluation
In the contemporary computational research landscape, scholars are often required to showcase findings derived from intensive computational experiments, sometimes involving up to 1 million CPU-hours or more. Given the accessibility of immense computational power through cloud infrastructures and cost-effective supercomputing clusters, executing extensive levels of calculations has become more practical. In a study published in the Journal of Computational Physics (JCP), I delineated the outcomes of an astounding 320,000 CPU-hours of rigorous computations, equivalent to approximately 10 million simulation iterations, introducing a nuanced methodology for the exhaustive assessment of closed-loop optimization performance.
Strategic Selection of Representative Models for Informed Decision-Making and Optimization Amidst Uncertainty
Uncertainty often manifests itself in the form of intricate probability distributions, necessitating the generation of numerous potential outcomes or realizations to fully encapsulate the inherent unpredictability. However, when faced with decision-making and optimization under such uncertain conditions, it becomes imperative to distill this overwhelming number of scenarios down to a concise, yet highly representative subset of models. Our research delves into the sophisticated methods of identifying the most emblematic models from a plethora of potential realizations, especially when critical decision variables remain indeterminate beforehand. This work has been documented in Computers & Geosciences.
Innovative Closed-Loop Field Development in Uncertain Environments Utilizing Optimization with Sample Validation
Our groundbreaking research, detailed in a paper featured in the SPE Journal, introduces a transformative approach to closed-loop field development (CLFD) under uncertainty, employing a novel technique known as Optimization with Sample Validation (OSV). Witness the compelling visualizations of our findings here. You can also find my research showcase here at Stanford smart fileds website.
Key Contributions from SPE 173219:
- Establishment of a pioneering CLFD optimization framework.
- Inception of Optimization with Sample Validation (OSV) for enhanced decision-making under uncertainty, applicable across numerous realizations derived from a probability distribution function.
- Introduction of a systematic OSV procedure that adeptly ascertains the requisite number of realizations for comprehensive uncertainty optimization.
- Demonstration of the robustness and efficiency of CLFD when integrated with OSV, proving instrumental for optimal decisions in hydrocarbon field development endeavors.
- Empirical evidence indicating that simultaneous optimization of multiple wells markedly outperforms conventional, isolated well-by-well strategies. View the evolution of water saturation maps contrasting these methodologies.
Imagine the possibilities if we could accurately simulate field development and reservoir management processes. Our research enables detailed simulation of these developments, accounting for sequential well drilling and the continuous influx of new, actionable data from each well.
Collaborating with my advisor, Prof. Louis Durlofsky, we've pioneered a revolutionary framework for field development optimization. CLFD epitomizes the synergy between history matching and optimization techniques, all geared towards maximizing oil recovery or net present value. The intricate workflow of CLFD is depicted in Figure 1.
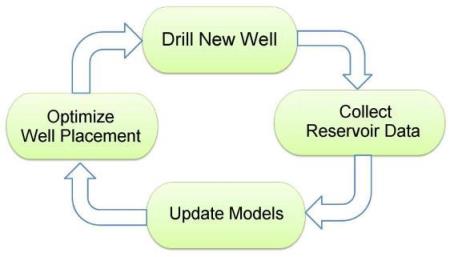
Figure 1: The Intricate Workflow of Closed-Loop Field Development (CLFD) Optimization, SPE 173219
The subject of "optimization under uncertainty" is critical, especially when dealing with high-stakes evaluations. Conventionally, uncertainty is addressed by utilizing a set of realizations. Our strategy, however, transcends this by implementing robust optimization across a select subset of representative realizations. This methodology, known as "optimization with sample validation" (OSV), involves rigorous validation criteria to confirm the adequacy of these realizations in representing the broader set. Our approach is tailored for scenarios where traditional stochastic programming techniques falter, offering a beacon of reliability for complex, computationally demanding optimization challenges.
Evaluating the Financial Worth of Hydrocarbon Reservoirs:
As illustrated in Figure 2, excerpted from Example 2 in the SPE-173219-PA study, our CLFD methodology plays a pivotal role in appraising the financial viability of petroleum reservoir development projects. By leveraging comprehensive data from existing wells, CLFD not only assesses but also enhances the project's value, particularly reflected in the P50 projections at subsequent stages.
The insights in Figure 2 underscore the significance of integrating reservoir data in refining decision-making throughout the reservoir development lifecycle. This integration not only elevates both the P10 and P50 projections consistently but also aligns the estimated project value (E[NPV], depicted in blue) closer to the P50 benchmark over time.
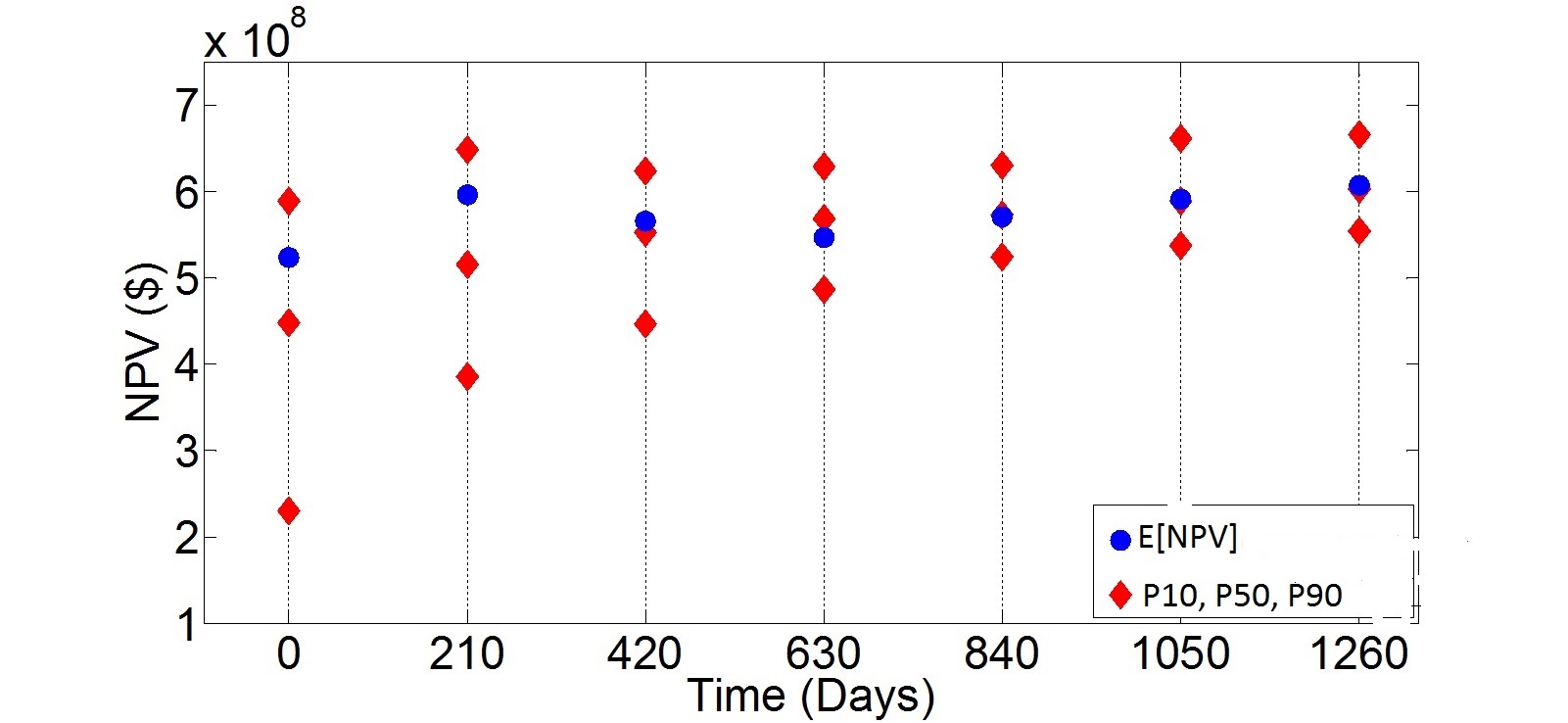
Figure 2: Projections of P10, P50, P90 NPVs (Net Present Values at 10th, 50th, and 90th percentiles) assessed across 50 realizations, juxtaposed with the expected NPV derived from a representative subset (of 10 realizations) through successive CLFD stages, SPE-173219-PA.
Advancing Large-Scale Inverse Problem Solving with TSVD-based Levenberg-Marquardt Algorithm
Our findings, published in a recent JPSE paper, delve into the construction and calibration of subsurface reservoir models in fields like hydrology and reservoir engineering, based on dynamic data such as flow rates observed at well locations.
Solving nonlinear inverse problems, prevalent in domains including geophysics, hydrology, signal processing, and machine learning, often involves seeking either a singular fitting model or multiple models encapsulating the inherent uncertainty. My research endeavors focus on unearthing efficient methodologies for addressing these nonlinear inverse conundrums.
The Levenberg-Marquardt algorithm stands out amidst various optimization algorithms for its prowess in resolving nonlinear inverse issues and is a favored technique in machine learning, especially for training sizable neural networks—a subject of our ongoing study. Our research confirms the algorithm's competency in yielding accurate solutions where other methods, like the Gauss-Newton and quasi-Newton, may falter by converging to imprecise model estimates.
Our innovation doesn't end there; we've tailored the Levenberg-Marquardt algorithm for large-scale applications. Utilizing TSVD (Truncated Singular Value Decomposition) parameterization, our algorithm determines the search direction by primarily considering the eigenvectors associated with the Hessian's largest eigenvalues, all without the need for computing the Hessian or Jacobian matrices. This refinement employs the Lanczos algorithm, negating the need for an explicit Jacobian computation and solely necessitating the product of the Jacobian with vectors. This strategic move not only enhances efficiency but also significantly reduces computational demands, making it ideal for training extensive neural networks.
Pioneering Efficiency in Comprehensive Field Development Optimization
In the realm of hydrocarbon field development, critical decisions are traditionally orchestrated using a symphony of optimization methods and reservoir simulation. These decisions delve into the granular details: the quantity of wells, their strategic placements, time-sensitive controls, the sequence of drilling, and the categories of wells involved. My research breaks new ground by introducing an optimized framework, meticulously engineered for the holistic optimization of these pivotal field development parameters.
Revolutionizing Reservoir Management with Gradient-based History Matching
At the heart of reservoir management lie computational models, architected to forecast the reservoir's future behavior patterns. These geological blueprints are crafted, drawing from a rich tapestry of geological, geophysical, and production data. With the reservoir continually unraveling new layers of data, the quest for proficient history matching methodologies has never been more paramount. History matching emerges as a crucial cog in the wheel of Closed-Loop Reservoir Management (CLRM), as depicted in Figure 3. CLRM not only offers a robust framework but also serves as a comparative arena where various history matching techniques can be evaluated on a level playing field.
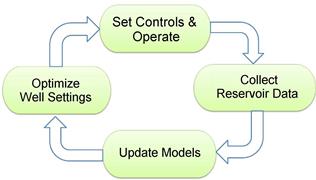
Figure 3: Schematic layout of closed-loop reservoir management
In this research, efficient gradient-based history matching techniques are developed for applications in closed-loop reservoir management. Figures 4 and 5, respectively, show data matches and predictions from prior and conditional RML realizations for a producer well. Data matches and predictions for the wells not shown are similar. As figure 5 shows, all RML realizations are generated in about 50 simulation runs which shows the efficiency of our gradient-based history matching technique.
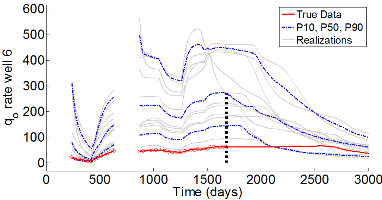
Figure 4: Data matches and predictions for unconditional realizations
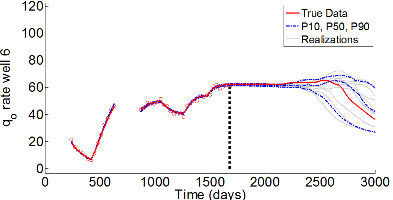
Figure 5: Data matches and predictions for conditional RML realizations. Dashed vertical line shows end of history matching.
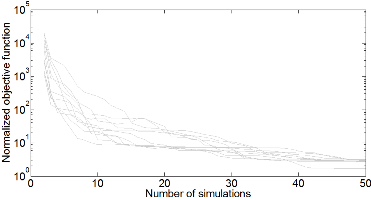
Figure 6: Normalized (history matching) objective function versus number of simulation runs.
Optimal Parameterization in Model Calibration
Employing parameterization based on a truncated Singular Value Decomposition (SVD) of a dimensionless sensitivity matrix stands out as an optimal approach in model calibration.
This technique hinges on the application of Gauss-Newton or Levenberg-Marquardt algorithms. While these gradient-based methods necessitate the computation of the sensitivity matrix, their applicability to large-scale model calibration challenges remains constrained. However, a strategic shift in parameterizing the model's change vector—in alignment with the eigenvectors linked to the Hessian matrix's largest eigenvalues—mandates just a truncated SVD of the sensitivity matrix, bypassing the need for the full matrix. Here, the Lanczos algorithm plays a pivotal role in computing a truncated SVD. Notably, for a matrix G, it demands only the product of G with a vector and the product of G’s transpose with a vector.
In the realm of model calibration, the sensitivity matrix G symbolizes the matrix of derivatives of the forecasted data in relation to all model parameters. Calculating the product of G with an arbitrary vector v is achievable through the gradient simulator method (direct method), whereas determining the product of G's transpose with an arbitrary vector u is attainable via an adjoint solution. It's imperative to understand that crafting the code for both the adjoint method and the gradient simulator method necessitates explicit knowledge of the reservoir simulator code.
It's noteworthy that while the adjoint method is renowned for its prowess in computing the analytical gradient from the simulator in model calibration, it also possesses the capability to compute the product of G’s transpose with any arbitrary vector u. For a specific vector u, the adjoint solution mirrors the analytical gradient.
However, a stumbling block arises with commercial reservoir simulators, which often lack provision for the adjoint/gradient simulator method. The absence of sensitivity matrix and analytical gradient information escalates computational expenses of model calibration, potentially undercutting reliability.
For an in-depth exploration of the results and the algorithms, this study in the Journal of Petroleum Science and Engineering serves as a comprehensive resource.
